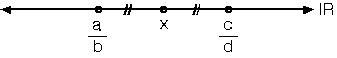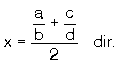BÖLME ve BÖLÜNEBİLME
A.BÖLME
A, B, C, K birer doğal sayı ve B 0 olmak üzere,
bölme işleminde,
• A ya bölünen, B ye bölen, C ye bölüm, K ya kalan denir.
• A = B . C + K dır.
• Kalan, bölenden küçüktür. (K <>
• Kalan, bölümden (C den) küçük ise, bölen (B) ile bölümün (C) yeri değiştirilebilir. Bu durumda K ile A değişmez.
• K = 0 ise, A sayısı B ile tam bölünebiliyor denir.
B. BÖLÜNEBİLME KURALLARI
1. 2 İle Bölünebilme
Birler basamağındaki rakamı çift olan sayılar 2 ile tam bölünür.
Tek sayıların 2 ile bölümünden kalan 1 dir.
2. 3 İle Bölünebilme
Rakamlarının sayısal değerleri toplamı 3 ün katı olan sayılar 3 ile tam bölünür.
Bir sayının 3 ile bölümünden kalan, rakamlarının toplamının 3 ile bölümünden kalana eşittir.
3. 4 İle Bölünebilme
Bir sayının onlar basamağındaki rakam ile birler basamağındaki rakamın (son iki basamak) belirttiği sayı, 4 ün katı olan sayılar 4 ile tam bölünür.
... abc sayısının 4 ile bölümünden kalan bc nin (son iki basamak) 4 ile bölümünden kalana eşittir.
• ... abc sayısının 4 ile bölümünden kalan
c + 2 . b nin 4 ile bölümünden kalana eşittir.
4. 5 İle Bölünebilme
Birler basamağındaki rakam 0 veya 5 olan sayılar 5 ile tam bölünür.
Bir sayının 5 ile bölümünden kalan, o sayının birler basamağındaki rakamın 5 ile bölümünden kalana eşittir.
5. 7 İle Bölünebilme
(n + 1) basamaklı anan-1 ... a4a3a2a1a0 sayısının 7 ile tam bölünebilmesi için,
k Z olmak üzere,
(a0 + 3a1 + 2a2) – (a3 + 3a4 + 2a5) + ... = 7k
olmalıdır.
Birler basamağı a0, onlar basamağı a1, yüzler basamağı a2, ... olan sayının (...a5a4a3a2a1a0 sayısının) 7 ile bölümünden kalan
(a0 + 3a1 + 2a2) – (a3 + 3a4 + 2a5) + ...
işleminin sonucunun 7 ile bölümünden kalana eşittir.
6. 8 İle Bölünebilme
Yüzler basamağındaki, onlar basamağındaki ve birler basamağındaki rakamların (son üç rakamın) belirttiği sayı 8 in katı olan sayılar 8 ile tam bölünür.
3000, 3432, 65104 sayıları 8 ile tam bölünür.
Birler basamağı c, onlar basamağı b, yüzler basamağı a, ... olan sayının (...abc sayısının) 8 ile bölümünden kalan c + 2 . b + 4 . a toplamının 8 ile bölümünden kalana eşittir.
7. 9 İle Bölünebilme
Rakamlarının toplamı 9 un katı olan sayılar 9 ile tam bölünür.
Bir sayının 9 ile bölümünden kalan, o sayının rakamlarının toplamının 9 ile bölümünden kalana eşittir.
8. 10 İle Bölünebilme
Birler basamağındaki rakamı 0 (sıfır) olan sayılar 10 ile tam bölünebilir. Bir sayının birler basamağındaki rakam o sayının 10 ile bölümünden kalandır.
9. 11 İle Bölünebilme
(n + 1) basamaklı anan–1 ... a4a3a2a1a0 sayısının 11 ile tam bölünebilmesi için
(a0 + a2 + a4 + ...) – (a1 + a3 + a5 + ...)... = 11 . k
ve k Z olmalıdır.
(n + 1) basamaklı anan–1 ... a4a3a2a1a0 sayısının 11 ile bölümünden kalan
(a0 + a2 + a4 + ...) – (a1 + a3 + a5 + ...)... işleminin sonucunun 11 ile bölümünden kalana eşittir.
C. BÖLEN KALAN İLİŞKİSİ
A, B, C, D, E, K1, K2 uygun koşullarda birer doğal sayı olmak üzere,
A nın C ile bölümünden kalan K1 ve
B nin C ile bölümünden kalan K2 olsun.
Buna göre,
• A . B nin C ile bölümünden kalan K1 . K2 dir.
• A ± B nin C ile bölümünden kalan K1 ± K2 dir.
• D . A nın C ile bölümünden kalan D . K1 dir.
• AE nin C ile bölümünden kalan K1E dir.
Burada kalan değerler bölenden (C den) büyük ise, tekrar C ile bölünerek kalan bulunur.
D. ÇARPANLAR İLE BÖLÜM
Bir A doğal sayısı B . C ile tam bölünüyorsa A sayısı B ve C doğal sayılarıyla da bölünebilir. Fakat bu ifadenin karşıtı (A sayısı B ile ve C ile tam bölünüyorsa A sayısı B . C ile tam bölünür.) her zaman doğru değildir.
144 sayısı 2 . 6 = 12 ile tam bölünür ve 144 sayısı 2 ile ve 6 ile de tam bölünür.
6 sayısı 2 ile ve 6 ile tam bölünür. Fakat 6 sayısı 2 . 6 = 12 ile tam bölünemez.
E. BİR TAM SAYININ TAM BÖLENLERİ
Bir tam sayının, asal sayıların çarpımı biçiminde yazılmasına bu sayının asal çarpanlarına ayrılması denir.
a, b, c birbirinden farklı asal sayılar ve m, n, k pozitif tam sayılar olmak üzere,
A = am . bn . ck olsun.
• A yı tam bölen asal sayılar a, b, c dir.
• A sayısının pozitif tam bölenlerinin sayısı:
(m + 1) . (n + 1) . (k + 1) dir.
• A sayısının pozitif tam sayı bölenlerinin ters işaretlileri de negatif tam sayı bölenidir.
• A sayısının tam sayı bölenleri sayısı:
2 . (m + 1) . (n + 1) . (k + 1) dir.
• A sayısının tam sayı bölenleri toplamı 0 (sıfır) dır.
• A sayısının pozitif tam sayı bölenlerinin toplamı:
• A sayısının asal olmayan tam sayı bölenlerinin sayısı, A nın tam sayı bölenlerinin sayısından A nın asal bölenlerinin sayısı çıkarılarak bulunur.
• A nın asal olmayan tam sayı bölenleri toplamı
– (a + b + c) dir.
• A sayısından küçük A ile aralarında asal olan sayıların sayısı:
• A sayısınının pozitif tam sayı bölenlerinin çarpımı:

 daima reeldir.
daima reeldir. daima reeldir.
daima reeldir.






































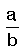
 Pay
Pay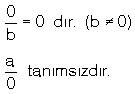
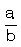 basit kesir ise
basit kesir ise 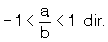
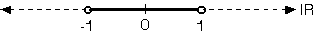
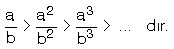
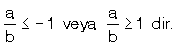


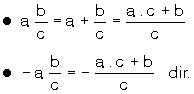
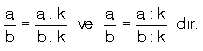
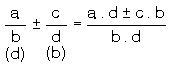
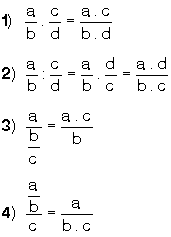
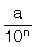 biçimindeki rasyonel sayılara ondalıklı sayı denir.
biçimindeki rasyonel sayılara ondalıklı sayı denir.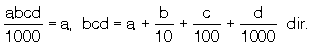
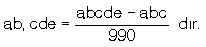
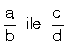 arasında sayılamayacak çoklukta rasyonel sayı vardır. Bunlardan bazılarını bulmak için b ile d nin OKEK i bulunur. Verilen kesirlerin paydaları bulunan OKEK inde eşitlenir. İstenen koşuldaki sayıyı bulmak için kesirler genişletilebilir.
arasında sayılamayacak çoklukta rasyonel sayı vardır. Bunlardan bazılarını bulmak için b ile d nin OKEK i bulunur. Verilen kesirlerin paydaları bulunan OKEK inde eşitlenir. İstenen koşuldaki sayıyı bulmak için kesirler genişletilebilir.